今天给大侠带来FIR数字滤波器设计,由于篇幅较长,分三篇。今天带来第二篇,FIR数字滤波器设计基础,包括FIR数字滤波器的特点、线性相位条件以及基本结构。话不多说,上货。
数字滤波器的输入输出均为数字信号,信号通过数字滤波器后,可以改变频率成分的相对比例或滤除某些频率成分。数字滤波器可以分为IIR数字滤波器和FIR数字滤波器。
本篇只介绍FIR数字滤波器的设计,可以根据所给定的频率特性直接设计FIR数字滤波器。FIR数字滤波器在保证幅度特性满足要求的同时,能够做到严格的线性特性。
本篇采用了窗函数法、频率采样法以及基于firls函数和remez函数的最优化方法设计FIR滤波器。对FIR滤波器进行了详细的理论分析,并且对应于每种方法都给出了设计实例。通过编写MATLAB语言程序,运行程序,得到幅频和相频特性图。
对于窗函数和firls函数设计的滤波器,还通过建立Simulink系统模块进行仿真,观察滤波器滤波情况。
FIR数字滤波器设计基础
一、FIR数字滤波器的特点
FIR滤波器在保证幅度特性的同时,很容易做到严格的线性相位特性。
在数字滤波器中,FIR滤波器的最主要特点是没有反馈回路,故不存在不稳定的问题。
同时,在幅度特性可以任意设置的同时,保证了精确的线性相位。
稳定和线性相位是FIR滤波器的突出优点。
另外还有以下特点:
- 设计方式是线性的;
- 硬件容易实现;
- 滤波器过渡过程具有有限区间;
- 相对IIR滤波器而言,阶次较高,其延迟也要比同样性能的IIR滤波器大得多。
二、FIR数字滤波器的线性相位条件
设滤波器单位脉冲响应的长度为N,系统函数为关系式(2-1),如下:
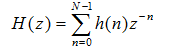
由此式可见,H(z)是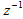 的(N-1)次多项式,它在Z平面上有(N-1)个零点,原点z=0是(N-1)阶重极点,位于r =1的单位圆内,系统永远稳定。稳定性和线性相位特性是FIR滤波器的突出优点。
的(N-1)次多项式,它在Z平面上有(N-1)个零点,原点z=0是(N-1)阶重极点,位于r =1的单位圆内,系统永远稳定。稳定性和线性相位特性是FIR滤波器的突出优点。
FIR滤波器的设计任务是选择有线长度的h(n),使传输函数 满足要求。
满足要求。
线性相位条件为关系式(2-2),如下:

对于长度为N的h(n),传输函数为关系式(2-3),如下:
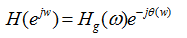
上式中,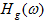 称为幅度特性,
称为幅度特性,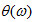 称为相位特性。线性相位是指相位函数
称为相位特性。线性相位是指相位函数 满足如下特性:
满足如下特性:
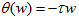
或
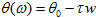
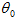 是起始相位,
是起始相位, 为常数,一般称第一种情况为第一类线性相位,称第二种情况为第二类线性相位。
为常数,一般称第一种情况为第一类线性相位,称第二种情况为第二类线性相位。
满足第一类线性相位的充要条件是:h(n)为实序列,并且对(N-1)/2偶对称,
即:
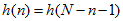 ;
;
满足第二类线性相位的充要条件是:h(n)为实序列,并且对(N-1)/2奇对称。
即:
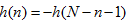 。
。
三、FIR数字滤波器的基本结构
FIR滤波器的基本结构有以下几种:直接型、级联型、线性相位型、频率采样型。
1、直接型
设FIR滤波器的单位冲击响应h(n)为一个长度为N的序列,则滤波器系统函数为关系式(2-4),如下所示:
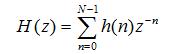
表示这一系统输入输出关系的差分方程为关系式(2-5),如下所示:
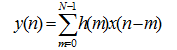
直接由差分方程可得出对应的网络结构如图2-1所示:

图2-1 FIR滤波器的直接型结构
直接型结构的优点:简单直观,乘法运算量较少。
缺点:调整零点较难。
2、级联型
当需要控制滤波器的传输零点时,可将H(z)分解为实系数二阶因子的乘积形式,见关系式(2-6),如下所示:
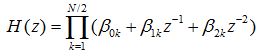
上式中, 为
为 的
的  变换,
变换, ,
, ,
, 为实数。级联型结构如图2-2所示:
为实数。级联型结构如图2-2所示:
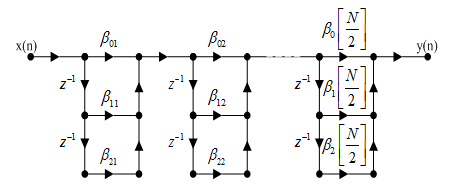
图2-2 FIR滤波器的级联型结构
该结构的优点:调整零点比直接型方便。
缺点: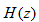 中的系数比直接型多,因而需要的乘法器多。当
中的系数比直接型多,因而需要的乘法器多。当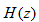 的阶次高时,也不易分解。
的阶次高时,也不易分解。
3、线性相位型结构
FIR滤波器的线性相位结构有偶对称和奇对称,不论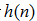 为偶对称还是奇对称都有:
为偶对称还是奇对称都有:
当N为偶数时,系统函数为关系式(2-7),如下所示:

当N为奇数时,系统函数为关系式(2-8),如下所示:
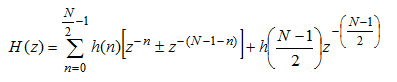
对这两种情况,都可以用FIR直接型实现,其信号流图如图2-3所示。
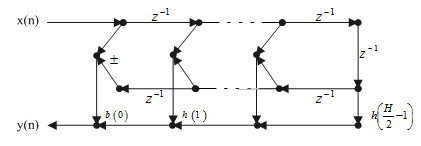
(a)N为偶数
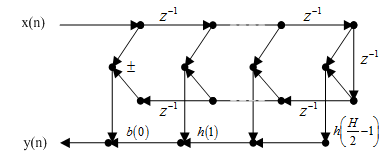
(b)N为奇数
图2-3 线性相位型结构
这种结构在本质上是直接型,但乘法次数比直接型省了一半。
4、频率采样型
频率采样型结构是一种用系数将滤波器参数化的一种实现结构。一个有限长序列可以由相同长度频域采样值惟一确定。
系统函数在单位圆上作N等分取样就是单位取样相应h(n)的离散傅里叶变换。 与系统函数之间的关系可用内插公式表示,为关系式(2-9),如下所示:
与系统函数之间的关系可用内插公式表示,为关系式(2-9),如下所示:
这样,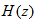 是由梳状滤波器和N个一阶网络的并联结构进行级联而成的,其网络结构(信号流图)如图2-3所示。是一个梳状网络,其零点为:
是由梳状滤波器和N个一阶网络的并联结构进行级联而成的,其网络结构(信号流图)如图2-3所示。是一个梳状网络,其零点为:
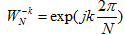 , k= 0, 1,2…,N-1
, k= 0, 1,2…,N-1
刚好和极点一样,等间隔地分布在单位圆上。理论上,极点和零点相互抵消,保证了网络的稳定性。
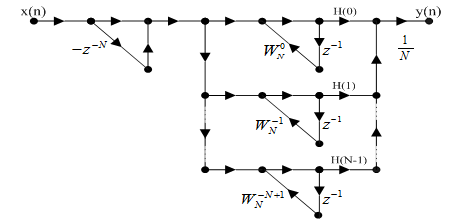
图2-5 FIR滤波器的频率采样结构
频率采样结构的优点:
1)在频率采样点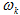 ,
,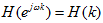 ,只要调整
,只要调整 就可以有效地调整频响特性。
就可以有效地调整频响特性。
2)只要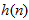 长度N相同,对于任何频响,其梳状滤波器部分和N个一阶网络部分完全相同,只是各支路增益
长度N相同,对于任何频响,其梳状滤波器部分和N个一阶网络部分完全相同,只是各支路增益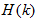 不同。相同部分便于标准化、模块化。
不同。相同部分便于标准化、模块化。
缺点:
1)寄存器长度都是有限的,零、级点可能不能正好抵消,造成系统不稳定。
2)当N很大时,其结构很复杂,需要的乘法器和延时单元很多。
第二篇就到这里,下一篇带来第三篇,FIR数字滤波器设计,包括窗函数法设计FIR滤波器、频率采样法设计FIR滤波器以及基于firls函数和remez函数的最优化方法设计FIR滤波器。
 芯耀
芯耀




 5620
5620
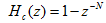 ,
,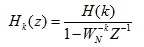

 下载ECAD模型
下载ECAD模型






