什么是极化函数和弥散函数？一文看懂量子化学中的“精度秘诀”

在量子化学计算中，我们经常会遇到一些看似复杂的基组符号，比如6-31G*、6-31G(d,p)、6-31+G(d,p)等等。这些符号背后其实隐藏着电子云行为的“微调机制”——极化函数（Polarization Function）和弥散函数（Diffuse Function）。

今天就带大家系统地了解一下它们是什么、为什么重要，以及在计算中该如何使用。

一、什么是“基函数”？

在量子化学计算中，我们要解决的是薛定谔方程，而方程的解（波函数）描述了电子的空间分布。但这个方程太复杂，几乎不可能直接求出解析解，因此我们需要“用一组已知的数学函数去逼近它”。这些用于构造波函数的数学函数就叫基函数（Basis Function）。由许多基函数组成的集合，就叫做基组（Basis Set）。

👉 可以这样理解：

每一个基函数就像一块“电子云积木”；
你用越多、越灵活的积木块，就越能拼出接近真实的电子分布。

在常见的基组体系中，STO-3G 或 6-31G 是最基础的。
其中“6-31G”表示：

内层电子用 6 个高斯函数拟合；
价层电子分为两部分（3 + 1），即所谓的“双ζ基组”或“劈裂价键基组”。

这种基组能较好地描述原子的基本电子结构，但仍然存在两个显著问题：

电子云太“僵硬” ——无法很好地反映键角、键长的细微变化；
电子分布太“集中” ——难以描述远离原子的电子行为。

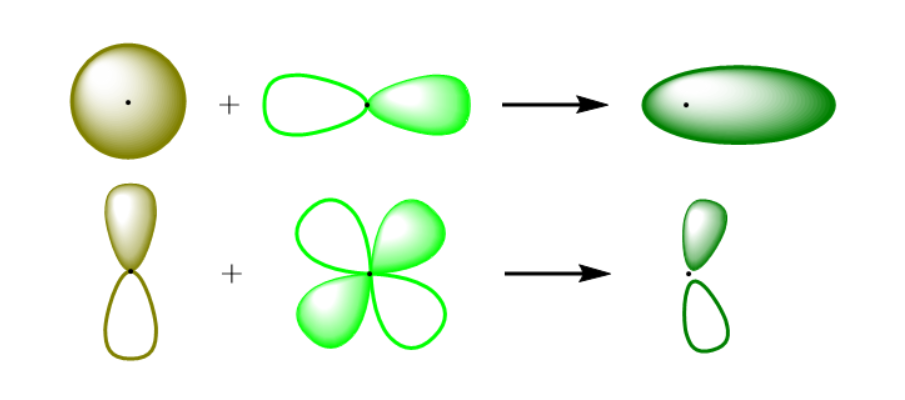
于是，科学家就在这些基础基组的“骨架”上做了两种改进：一种是让电子云能“形变”（极化函数），另一种是让电子云能“飘远”（弥散函数）。

二、极化函数

在真实体系中，电子云并不是一个固定不动的球体。当分子形成化学键、受外场或与其他原子相互作用时，电子云会被拉伸、偏移或极化。而基础基组（如6-31G）往往假设电子云是刚性的，不能随环境变化而形变。因此，我们需要为它“增加形变能力”——这就是极化函数（Polarization Function）的作用。

🔬 1. 极化函数的原理

极化函数的本质是在基组中添加更高角动量的轨道。
例如：

对氢（H）这种只有 s 轨道的原子，加入 p 轨道函数；
对碳、氧、氮等第二周期元素，加入 d 轨道函数；
对过渡金属元素，则可加入 f 轨道函数。

这些额外的函数本身在基态中没有电子占据，但它们允许电子波函数在外界扰动下发生偏移，从而更真实地反映化学键的极化和分子间的电荷重新分布。

🧮 2. 表示方法与符号含义

极化函数通常用“*”或“(d,p)”表示。

6-31G* ：只对重原子加极化函数（例如碳、氧）；
6-31G**：对重原子和氢原子都加上极化函数。

🌟 多一个“*”，就代表多考虑了一层电子形变。
这类基组在描述几何构型、偶极矩、振动频率时会显著提高精度。

🧫 3. 举个实际的例子

以水分子为例，若仅用 6-31G 基组计算，其 O–H 键长会略短、键角偏大。但加入极化函数（6-31G(d,p)）后，计算出的键长与实验值几乎吻合。原因就在于极化函数让电子云在氧原子附近能随氢原子方向“偏移”——更接近真实的极化效应。

三、弥散函数

如果说极化函数让电子云能变形，那么弥散函数让电子云能“变大”。在一些体系中，电子并不总是紧紧围绕原子核分布。

比如阴离子、氢键、范德华相互作用体系，电子分布往往比较“松散”，甚至延伸到较远的空间。普通基组的函数太集中，无法描述这些“远离核区”的电子行为。这时候，就要引入弥散函数（Diffuse Function）。

1. 数学原理

高斯型基函数的形式为：

ψ(r)=e−αr2psi(r) = e^{-alpha r^2}

其中 α 控制函数的“宽度”：

α 大 → 函数紧密集中；
α 小 → 函数扩散延伸。

弥散函数就是选取α 较小的高斯函数，让电子云分布得更宽、更远。
这样可以更好地描述电子的离域效应和弱相互作用。

2. 表示方法与符号

弥散函数用“+”号来表示：

6-31+G(d) ：对重原子加入弥散函数；
6-31++G(d,p) ：对重原子和氢原子都加上弥散函数。

➕ 多一个“+”，电子云“飘”得更远。
这在计算阴离子、分子复合物或氢键体系时尤为重要。

3. 应用实例

阴离子体系：
没有弥散函数，电子可能会被“挤回”原子核附近，导致能量偏高。
非键相互作用体系（如分子间氢键）：
弥散函数能准确描述弱电荷分布和相互作用能。