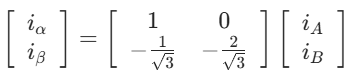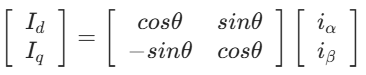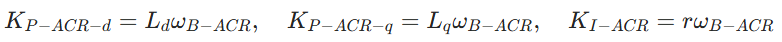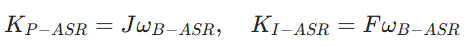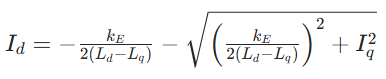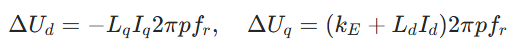矢量控制是永磁同步电机(PMSM)高精度、高效率控制的核心技术,ST MC SDK 5.x 作为 STM32 电动机控制的官方开发套件,将矢量控制理论与工程实现深度融合。本文基于 STM32 电动机控制系列讲座核心内容,从电机原理、矢量变换、控制架构、SVPWM 技术到进阶算法,系统拆解 ST MC SDK 5.x 的矢量控制理论基础,为开发者提供 “理论 + 实战” 的完整指引。
资料获取:如何配置STM32MP257的RMII Switch
1. 核心思想:交流电机的 “直流化” 控制
矢量控制的本质的是将三相交流电动机等效为他励直流电动机,通过坐标变换实现转矩与励磁的独立解耦控制,核心逻辑如下:
- 定子电流分解:将三相定子电流(Ia、Ib、Ic)通过坐标变换,分解为两个正交分量 —— 直轴电流 Id(励磁电流,控制磁场强度)和交轴电流 Iq(转矩电流,控制输出转矩);
- 独立闭环控制:对 Id 和 Iq 分别设计 PI 调节器,实现磁场与转矩的精准独立控制,从而获得与直流电机相当的动态响应和控制精度;
- 适配永磁同步电机:结合 PMSM 的永磁励磁特性,优化电流分配策略,兼顾效率与动态性能。
2. 永磁同步电机核心原理与数学模型
2.1 转动原理
PMSM 的转动依赖两种力矩协同作用:
- 永磁力矩:由永磁体产生的磁场与定子电流磁场相互作用生成;
- 磁阻力矩:由定子电流磁场导致电机磁阻变化产生(当 Ld≠Lq 时显著);
- 核心条件:电机电角速度 ωe 与机械角速度 ωr 满足 ωe = pωr(p 为电机极对数),确保定子磁场与转子磁场同步旋转。
2.2 数学模型(dq 坐标系)
PMSM 的电压方程是矢量控制的理论基石,dq 坐标系下核心方程如下:
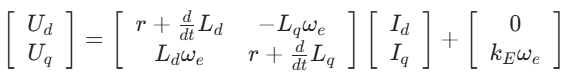
- 关键参数:r 为定子绕组电阻,Ld/dq 为直轴 / 交轴电感,kE 为反电动势系数,ωe 为电角速度;
- 耦合项:方程中 - LqIqωe 和 LdIdωe 为 dq 轴间的耦合项,需通过控制算法(如前馈控制)补偿,确保解耦效果。
3. 矢量变换:坐标转换的核心步骤
矢量变换是实现 “交流直流化” 的关键,ST MC SDK 5.x 通过标准化函数实现 Clarke 变换与 Park 变换,流程如下:
3.1 变换逻辑与公式
- Clarke 变换:将三相静止坐标系(ABC)的电流转换为两相静止坐标系(αβ),简化计算复杂度:
- Park 变换:将两相静止坐标系(αβ)的电流转换为两相旋转坐标系(dq),实现转矩与励磁解耦(θ 为 dq 轴与 αβ 轴的夹角,与电机转子位置同步):
- 逆 Park 变换:将 dq 坐标系的电压指令转换为 αβ 坐标系,为 SVPWM 提供输入。
3.2 SDK 实现方式
ST MC SDK 5.x 在mc_math.c文件中提供标准化变换函数,直接调用即可:
- Clarke 变换:
MCM_Clarke(Curr_Components Curr_Input); - Park 变换:
MCM_Park(Curr_Components Curr_Input, int16_t Theta); - 逆 Park 变换:
MCM_Rev_Park(Volt_Components Volt_Input, int16_t Theta); - 文件路径:
xxxMCSDK_v5.2.0MotorControlMCSDKMCLibAnySrc。
4. 矢量控制架构:双环 PI 调节与解耦
4.1 控制框图核心组成
矢量控制系统采用 “速度环 + 电流环” 的双闭环架构,核心环节包括:
- 速度调节器(ASR):输入速度指令与实际速度差值,输出转矩电流 Iq 指令;
- 电流指令发生器:结合 MTPA、弱磁控制策略,生成 Id 和 Iq 的目标值;
- 电流调节器(ACR):对 Id、Iq 的指令值与反馈值差值进行 PI 调节,输出 Ud、Uq 电压指令;
- 解耦前馈计算器:补偿 dq 轴间的耦合项,提升控制精度;
- 矢量变换与逆变换:实现坐标转换与指令传递。
4.2 PI 参数设定(SDK 适配)
ST MC SDK 5.x 提供明确的 PI 参数计算公式,兼顾理论与工程实现:
- 电流环 PI 参数(基于电机参数):
其中 ωB-ACR 为电流调节器通带宽度; - 速度环 PI 参数(基于机械参数):
其中 J 为转动惯量,F 为阻力系数,ωB-ASR 为速度调节器通带宽度; - SDK 参数位置:PID 参数定义在
drive_parameters.h文件中,如PID_TORQUE_KP_DEFAULT(转矩环 KP)、PID_SPEED_KI_DEFAULT(速度环 KI)。
4.3 SDK 实现文件
- PI 调节器核心函数:
pid_regulator.c中的PI_Controller(PID_Handle_t *pHandle, int32_t wProcessVarError); - 解耦控制:集成在电流调节器中,通过前馈项补偿耦合电压。
5. 空间电压矢量 PWM(SVPWM):指令执行核心
SVPWM 是将 dq 坐标系电压指令转换为电机定子三相驱动电压的关键技术,相比传统 SPWM,具有电压利用率高、谐波失真小的优势。
5.1 核心原理
- 电压矢量合成:将 αβ 坐标系的电压指令(Uα、Uβ)分解为 6 个非零基本电压矢量和 2 个零矢量的组合;
- 扇区判断:根据 Uα、Uβ 计算 X、Y、Z 值,确定电压矢量所在扇区(共 6 个扇区);
- 时间分配:计算各基本矢量的作用时间,确保合成电压与指令电压一致;
- 脉冲生成:根据扇区和时间分配,生成三相 PWM 脉冲信号。
5.2 SDK 实现方式
- 核心函数:
pwm_curr_fdbk.c中的PWMC_SetPhaseVoltage(PWMC_Handle_t *pHandle, Volt_Components Valfa_beta); - 关键步骤:函数内部自动完成扇区判断、时间计算与 PWM 生成,无需手动编写底层逻辑;
- 适配特性:支持不同电机极对数、PWM 频率配置,兼容 STM32 各系列 MCU 的定时器外设。
6. 进阶优化算法:提升控制性能的关键
ST MC SDK 5.x 集成三大核心优化算法,针对不同应用场景提升电机控制性能,均以库函数形式提供调用:
6.1 每安培最大转矩(MTPA)
- 核心目标:在输出相同转矩的前提下,最小化定子电流,提升电机效率;
- 核心公式:当 Ld<Lq 时,最优 Id、Iq 满足:
- SDK 实现:头文件
max_torque_per_ampere.h,自动计算最优电流分配方案。
6.2 弱磁控制
- 核心目标:突破电机额定转速限制,实现高速运行(当电机转速超过额定值时,反电动势升高,需削弱磁场降低反电动势);
- 约束条件:电压约束
与电流约束
;
- SDK 实现:头文件
flux_weakening_ctrl.h,自动调整 Id 电流削弱磁场,扩展转速范围。
6.3 电流前馈控制
- 核心目标:补偿 dq 轴间的耦合电压,提升动态响应速度,减少 PI 调节器负担;
- 补偿公式:
其中 fr 为电机机械频率; - SDK 实现:头文件
feed_forward_ctrl.h,实时计算耦合补偿电压并叠加到 PI 输出指令中。
7. 核心总结与实战建议
ST MC SDK 5.x 的矢量控制理论体系可概括为 “解耦为核心,变换为工具,双环控制为骨架,优化算法为提升”,实战开发中需注意:
- 先完成电机参数辨识(如 r、Ld、Lq、kE),确保 PI 参数与算法计算的准确性;
- 优先调用 SDK 标准化函数(如变换、SVPWM、MTPA),避免重复开发底层逻辑;
- 根据应用场景选择优化算法:效率优先场景启用 MTPA,高速场景启用弱磁控制,动态响应优先场景启用电流前馈;
- 调试重点:先调试电流环确保 Id、Iq 解耦正常,再调试速度环,最后启用优化算法。
 芯耀
芯耀



 1970
1970