量化计算能量震荡的处理方法

量化计算中，涉及在柔性体系以及大体系的计算时（td激发态计算也常常出现能量震荡），经常出现能量震荡导致结构难以正常结束。本文将介绍处理能量震荡的一般解决方法。首先需要了解能量震荡的本质是什么，量化计算的本质就是在势能面上搜索能量最小点，但是实际上势能面并不是如下面右图中的鞍点一样平滑。真实的情况是势能面上遍布“势阱“（即局部能量最小值点）。当梯度算法无法跳出势阱在其边缘”震荡“的表现（如图2）。

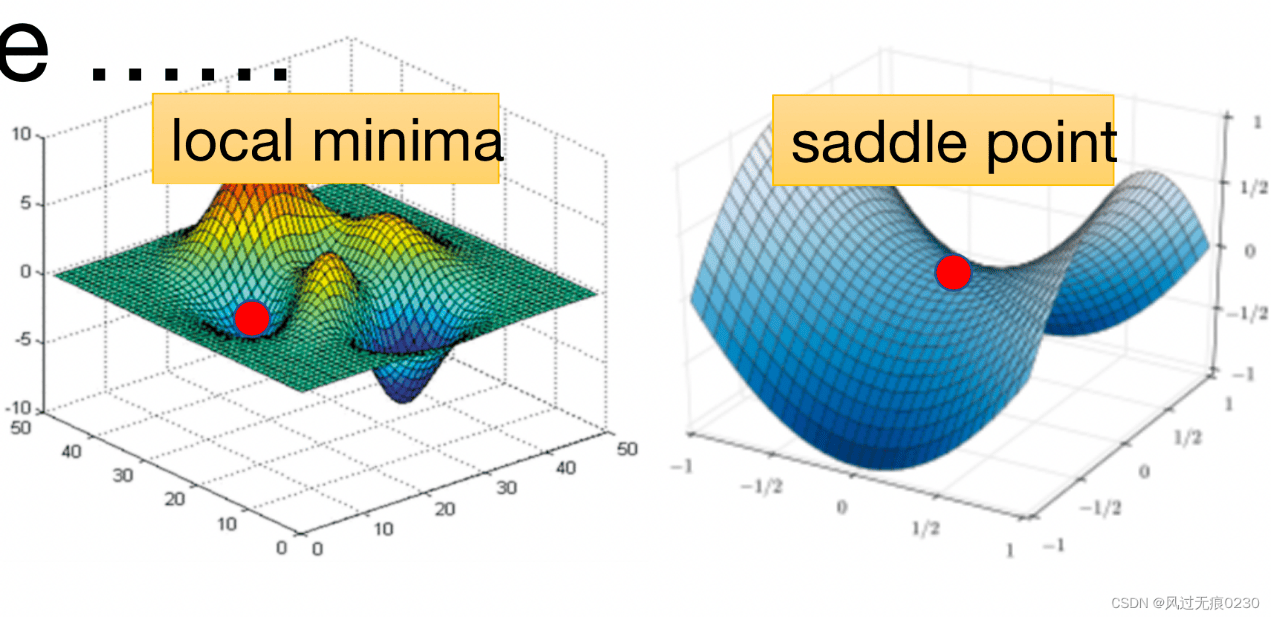
图1. 势能面示意图

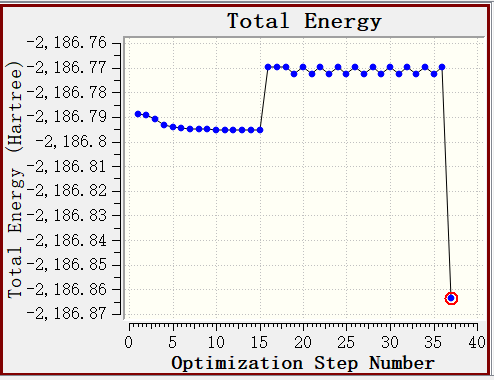
图2. 典型的能量震荡案例

一般解决能量震荡的方法如下

1、 使用maxstep=N关键词降低步长，高斯默认N=30，在遇到能量震荡的情况下时，可以降低优化步长，如maxstep=5。

2、提高积分格点精度例如int=ultrafine，在使用 DFT 泛函（尤其是 M06-2X, ωB97XD 等含色散矫正的泛函）计算时，积分的误差可能导致势能面出现微小的局部能量最小值点，使得计算在这些”小坑”里“反复横跳“。

3、使用不同的坐标定义方式，内坐标或笛卡尔坐标。

4、更换泛函和基组进行结构优化，然后读取波函数文件（chk文件），使用优化好的结构坐标用原泛函和基组再次提交结构优化任务。

5、 更改收敛标准，使用loose关键词放宽收敛限。

6、 微微调整结构（二面角，键角等参数）。